简单的自编码器
从函数拟合的角度看机器学习
在之前的活动中,我们介绍了神经网络的具体结构,这次我们从更抽象(潦草)的角度看待机器学习的任务。
在数学上,机器学习的核心任务可以被理解为寻找一个函数来拟合数据:
其中:
- 是输入数据,
- 是期望的输出,
- 是模型的参数,
- 是一个高维的、可能极其复杂的函数。
这个函数可以是:
- 线性函数(线性回归)
- 多项式函数(非线性回归)
- 神经网络(深度学习)
- 高斯过程(贝叶斯方法)
- 核方法(SVM)
我们的目标是找到一个最优的 使得它在训练数据和测试数据上都能很好地拟合(泛化能力强)。
为什么我们选择深度学习?
下面的内容大量参考了苏剑林老师的博客 科学空间|Scientific Spaces 中的内容
所有机器学习模型之中,也许最有趣、最深刻的便是神经网络模型了。
不过其实深度学习的可解释性是很差的,你很难从神经网络的参数中看出来,它到底在做什么事情。而很多其他的方法好像都经过了精心设计,让人安心。那深度学习这个令人不安的模型,有什么优势呢?
或许在于它尝试解决了下面的问题:
这个函数应该是什么?
你可能要问了,这个问题不是很基础吗,难不成只有深度学习才能回答?
事实上,在深度学习出现以前,模型和特征的选取,基本都是人工选择的。传统的模型,如线性回归、逻辑回归,基本都是我们人工指定这个函数的形式,可是非线性函数那么多,简单地给定几个现成的函数,拟合效果往往有限,而且拟合效果很大程度上取决于找到了良好的特征。
举个例子来说,一个函数如果是 ,是二次的非线性函数,那么如果用线性回归来拟合它,那么效果怎么也不会好的,可是,我定义一个新的特征 ,那么 是关于 的线性函数,这时候用线性模型就可以解决它,问题是在不知道 的具体形式下,怎么找到特征 呢?这基本靠经验和运气了。
而深度学习的算法是用来发现良好的特征的,这部分工作,以前通常都只是靠人工来选取,而且选取的效果不一定“良好”。现在,机器能够自动(无监督地)完成这个事情,实现的效果还不比人工选取的差,甚至线性模型都可以有不错的表现。
更进一步的技术细节就不在这里讨论了,如果你想去了解为什么神经网络可以提取特征,可以看这个视频: 【官方双语】深度学习之神经网络的结构 Part 1 ver 2.0_哔哩哔哩_bilibili 如果你想了解我们是怎么让神经网络去“学习” 的,可以看我们 BP 教学例会的总结 用 numpy 实现的手写数字识别的分类模型。当然,网络上关于神经网络的讲解太多太多了,相信你学习这方面的内容并不困难。
分类模型到生成模型
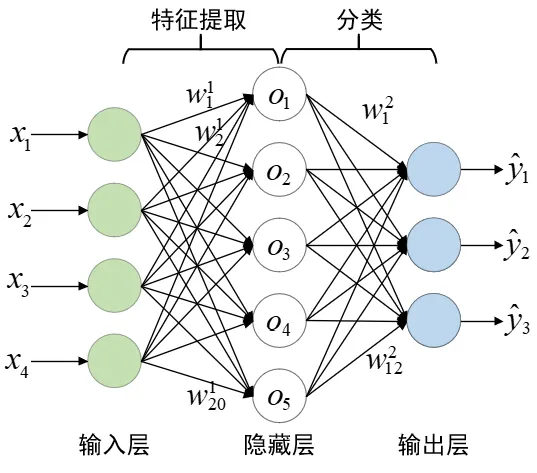
提取特征然后进行分类听起来并不是个很困难的事情,一个更有趣的挑战是,怎么让模型生成新的数据?
比如说我有很多手写数字的图片,怎么让模型学会这一系列数字的写法,生成更多张手写数字呢?
(这里我们降低点要求,不要求模型可以生成指定数字的图片,只要生成 0-9 任意数字的图片即可)
一个很自然的想法是,既然我可以训练一个神经网络提取到数据的特征,那么我们是不是可以再训练一个神经网络,将特征还原为数据呢?就像这样:
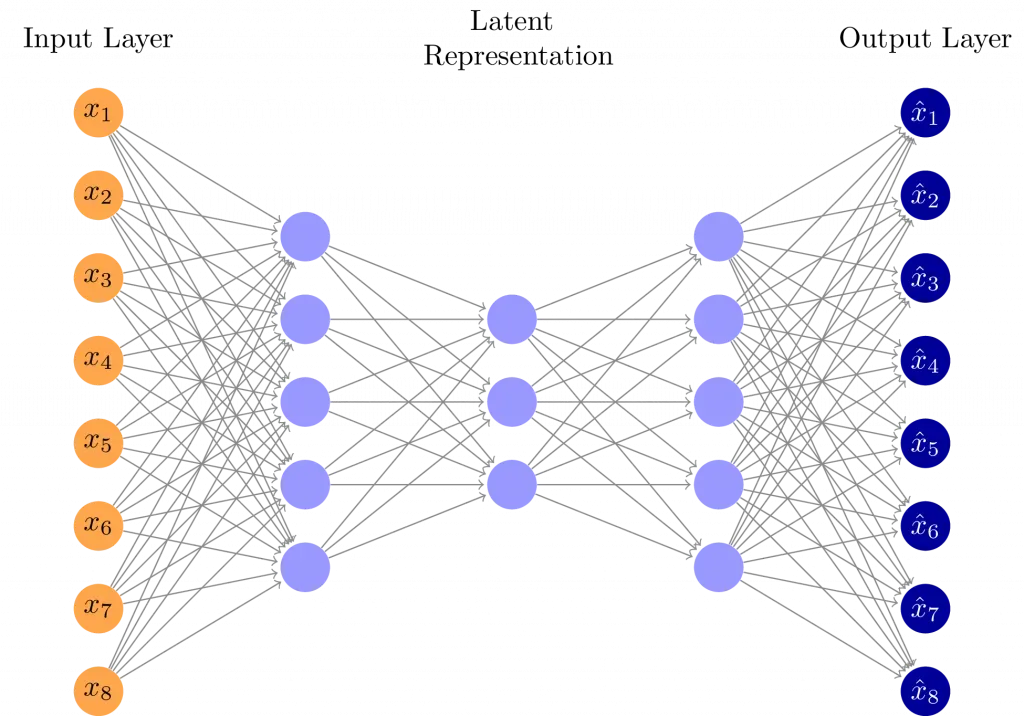
我们把左半边的网络叫做编码器,它的任务是提取高维数据(图片)中的特征,输出低维的隐变量 ;右半边的网络叫做解码器,它的任务是根据隐变量 把数据重构出来。
我并不确定这个隐变量 是不是真的可以代表特征,但是可以把它当作提取到的特征来理解。

训练的时候我们希望对于每张图片,重构出来的数据和原来的数据要尽量相等。那么训练好了之后,我们在低维的隐空间随便采样一个 , 是不是就可以通过解码器生成数据了呢?
实践出真知,我们来训练一个模型试试看吧!
这里省略了数据集的加载和超参数的设置,完整代码可以在社团仓库下载。
不想看代码可以 直接看结果,你只需要知道编码器把 784 维的图片(28x28 像素)编码到仅仅 8 维的隐变量 z ,解码器用 z 把整张图片还原。
模型定义:
class AutoEncoder(nn.Module):
def __init__(self):
super().__init__()
# 设置隐藏层神经元的数量(即潜在表示的维度)
self.num_hidden = 8
# 定义自编码器的编码器部分
self.encoder = nn.Sequential(
nn.Linear(784, 256), # 输入维度 784(28x28 像素),映射到 256 维
nn.ReLU(), # 采用 ReLU 激活函数,引入非线性
nn.Linear(256, self.num_hidden), # 进一步压缩到 num_hidden 维
nn.ReLU(), # 再次使用 ReLU 激活函数,增强特征表达能力
)
# 定义自编码器的解码器部分
self.decoder = nn.Sequential(
nn.Linear(self.num_hidden, 256), # 从 num_hidden 维度恢复到 256 维
nn.ReLU(), # 采用 ReLU 激活函数,引入非线性
nn.Linear(256, 784), # 从 256 维恢复到 784 维,与原始输入大小一致
nn.Sigmoid(), # 使用 Sigmoid 将输出值压缩到 (0,1) 范围,适用于归一化后的像素数据
)
def forward(self, x):
"""
前向传播过程:
1. 输入数据经过编码器,得到潜在空间表示(encoded)
2. 潜在表示再通过解码器,恢复为原始输入的近似值(decoded)。
"""
encoded = self.encoder(x) # 通过编码器得到潜在表示
decoded = self.decoder(encoded) # 通过解码器恢复原始数据
return encoded, decoded # 返回潜在表示和重建的输出模型训练:
num_epochs = 10
for epoch in range(num_epochs):
total_loss = 0.0 # 记录当前 epoch 的总损失
for batch_idx, data in enumerate(train_loader):
# 获取一个批次的训练数据,并将其移动到指定设备(CPU/GPU)
data = data.to(device)
# 前向传播:通过编码器和解码器获取输出
encoded, decoded = model(data)
# 计算损失(重构误差),然后进行反向传播
loss = criterion(decoded, data) # 目标是使 decoded 尽可能接近原始输入 data
optimizer.zero_grad() # 清空梯度,防止梯度累积
loss.backward() # 计算梯度
optimizer.step() # 更新模型参数
# 累积损失
total_loss += loss.item() * data.size(0)
# 计算并打印当前 epoch 的平均损失
epoch_loss = total_loss / len(train_loader.dataset)
print(
"Epoch {}/{}: loss={:.4f}".format(epoch + 1, num_epochs, epoch_loss)
)
训练完成看看效果
先来看看 loss
Epoch 1/10: loss=0.0514
Epoch 2/10: loss=0.0380
Epoch 3/10: loss=0.0322
Epoch 4/10: loss=0.0304
Epoch 5/10: loss=0.0293
Epoch 6/10: loss=0.0286
Epoch 7/10: loss=0.0281
Epoch 8/10: loss=0.0277
Epoch 9/10: loss=0.0273
Epoch 10/10: loss=0.0270看起来很正常
然后抽取测试集的前 10 张图片进行测试
原图:

重构后图像:

对于一个简单的网络来说,这个效果已经可以令人满意了。
可以看到图片变模糊了,这可以理解,毕竟我们是通过仅仅 8 个维度的隐变量 还原了这些图片。一般来说增加隐藏单元的数量将提高图像质量,而减少隐藏单元的数量会使模糊变得更糟。
talk is cheap, 我们来看看 4 个维度的效果:
这是 loss:
Epoch 1/10: loss=0.0612
Epoch 2/10: loss=0.0509
Epoch 3/10: loss=0.0481
Epoch 4/10: loss=0.0467
Epoch 5/10: loss=0.0459
Epoch 6/10: loss=0.0452
Epoch 7/10: loss=0.0447
Epoch 8/10: loss=0.0442
Epoch 9/10: loss=0.0438
Epoch 10/10: loss=0.0435这是重构的图像:似乎这个模型很喜欢 9

可以看到重构的质量明显变差了。
当然,隐空间的维度也不能太大,假设隐空间的维度和图片相同,那么编码器和解码器的最优解就是沆瀣一气,将模型退化为恒等映射。这样的话何谈生成模型呢?
是否可以生成新的图片
我们的模型可以重构图片,但是是否可以真的去生成图片呢?
回过头来看一下我们的模型做了什么:
这些手写数字的数据存在于高维空间(784 维),我们用编码器提取特征将其变为了 8 维空间的隐变量 , 然后解码器可以通过隐变量还原图片。
因此我们通过训练集和编码器计算出来的 , 是低维空间的一系列的点。如果我们想要通过采样得到的 生成随机的新图片,就必须去研究 背后是什么样的一个分布。
下面是采样 1000 个训练集图片,通过编码器计算出来的 的分布。
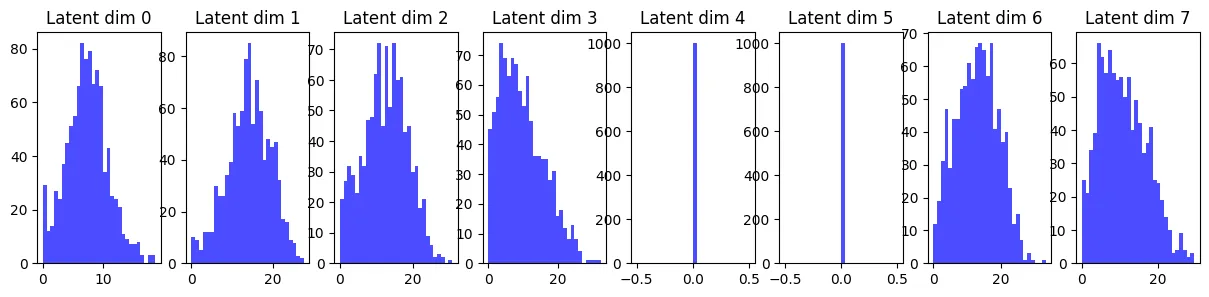
emmm, 似乎有两个维度在摸鱼,这是常见的维度塌陷问题。
再来看看前两个维度的分布,不同颜色代表不同的数字
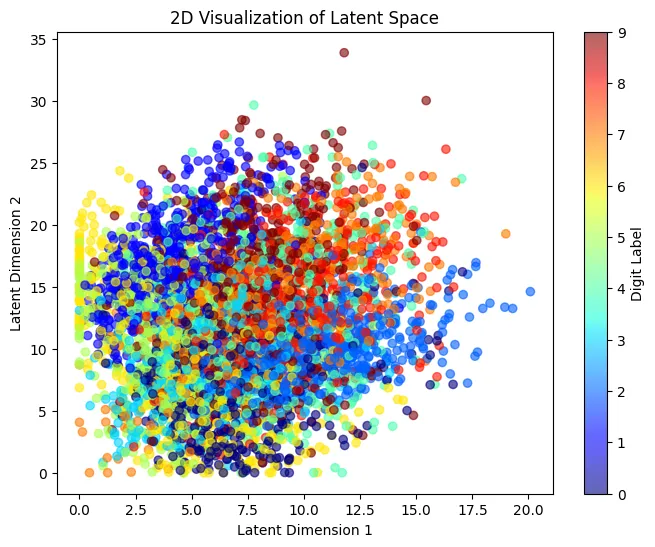
不得不说有些混乱
根据这些图像,我们在将 4,5 维度置为 0,其他维度以 采样,得到了下面的结果:
肉眼观察分布再进行采样确实是一个奇怪的操作,但是这里我们没有更好的办法。

有些样本还算正常,但是其他的基本看不出来是什么。
并且随着维度的升高,采样会变得越来越困难,非常容易得到下面的结果:

数字已经无法辨认,而且你必须进行更长时间的采样才能获得视觉上有意义的东西。
所以很遗憾,我们这个简单的模型生成新图片的能力很差。
总结
为什么我们这个简单的编解码器在重构的时候还算令人满意,但是生成新图像的能力很差呢?
以及有没有更好的方法生成图片?
这些问题在下周的 VAE workshop 将得到解答。
引用声明
本文章参考了以下文章和资料,特此致谢。所有引用内容归原作者所有,如有侵权,请联系删除。
代码参考 Implementing Variational Autoencoders from scratch | by Konstantin Sofeikov | Medium